From the top of a 7 m high building, the angle of elevation of the top
Trigonometry (10)From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Answer
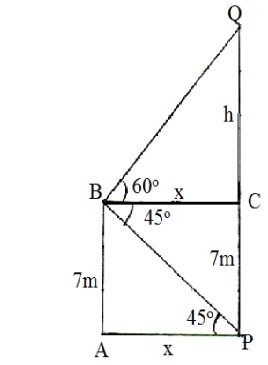
$$ \text{In } \triangle ABP, \tan 45^0 = \frac{7}{x} \Rightarrow x = 7 $$
$$ \text{In } \triangle BCQ, \tan 60^0 = \frac{h}{x} \Rightarrow h = \sqrt{3} x $$
$$ h = 7\sqrt{3} m $$
$$ \text{Height of tower } = PQ = 7 + h $$
$$ = 7+ 7\sqrt{3} = 7(1+\sqrt{3}) m $$
- Exam Year: 2023
Related Questions
- Amit, standing on a horizontal plane, finds a bird flying at a distance of 200 m from him
- The shadow of a tower standing on a level ground is found to be 40 m
- Evaluate: (3 sin 43°/cos 47°)^2
- If a tower 30 m high, casts a shadow $10\sqrt{3}$ m long on the ground
- As observed from the top of a 100 m high light house
- If $ \triangle ABC \sim \triangle DEF $ and $ \angle A = 47^{\circ}, \angle E = 83^{\circ} $