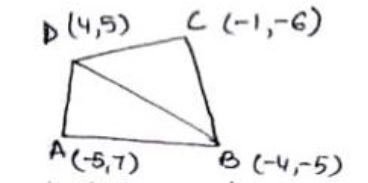
If A(-5, 7), B(-4, -5), C(-1, -6) and D(4, 5) are the vertices of a quadrilateral
Coordinate Geometry (10)If A(-5, 7), B(-4, -5), C(-1, -6) and D(4, 5) are the vertices of a quadrilateral, find the area of the quadrilateral ABCD.
Answer
Area of quad ABCD = Ar ΔABD + Ar ΔBCD
Area of ΔABD = $\frac{1}{2}$ |(-5)(-5 - 5) + (-4)(5 - 7) + (4)(7 +5)|
= 53 sq units
Area of ΔBCD = $\frac{1}{2}$ | (-4)(-6-5)+ (-1)(5 +5)+4(-5+6)|
= 19 sq units
Hence, area of quad. ABCD = 53 + 19 = 72 sq units
- Exam Year: 2018
Related Questions
- If the points A(2, 3), B(-5, 6), C(6, 7) and D(p, 4) are the vertices
- Find the area of a triangle whose vertices are given as (1, -1) (-4, 6) and (-3, -5)
- Find a relation between x and y if the points A(x, y), B(-4, 6) and C(-2, 3) are collinear
- Find the ratio in which the line x - 3y = 0 divides the line segment
- Find the coordinates of the point which divides the join of A(-1, 7) and B(4, -3) in the ratio 2 : 3
- If A(-2, 1), B(a, 0), C(4, b) and D(1, 2) are the vertices of a parallelogram ABCD