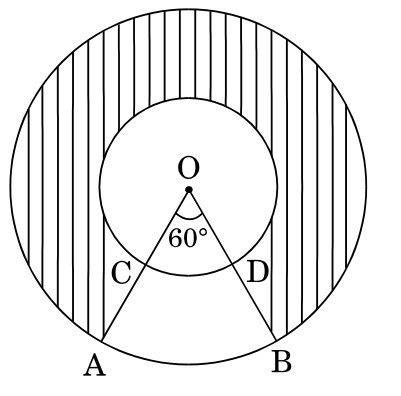
In the given figure, two concentric circles with centre O have radii 21 cm and 42 cm

In the given figure, two concentric circles with centre O have radii 21 cm and 42 cm. If  $\angle$ AOB = $60^{\circ}$, find the area of the shaded region.

Use π = $\frac{22}{7}$

• Answer:

  Area of region ABDC = π$\frac{60}{360}$x(42² - 21²)

  $$ = \frac{22}{7} \times \frac{1}{6} \times 63 \times 21 $$

  = 693 cm²

  = Area of shaded region = π(42² - 21²) - region ABDC 

  $$ = \frac{22}{7} \times 63 \times 21 - 693 $$

  = 4158 - 693

  = 3465 cm²

• Exam Year: 2017