In what ratio does the point (24/11, y) divide the line segment joining the points P(2, - 2) and Q(3, 7)
Coordinate Geometry (10)In what ratio does the point (24/11, y) divide the line segment joining the points P(2, -2) and Q(3, 7) ? Also find the value of y.
Answer
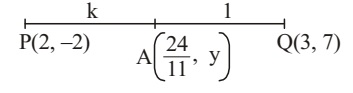
Let PA : AQ = k : 1
$$ \frac{2+3k}{k+1} = \frac{24}{11} $$
$$ K = \frac{2}{9} $$
Hence, the ratio is 2 : 9
$$ y = \frac{-18+14}{11} = \frac{-4}{11} $$
- Exam Year: 2017
Related Questions
- Use of mobile screen for long hours makes your eye sight weak and give you headaches
- Write the coordinates of a point P on x-axis which is equidistant
- If the distances of P(x, y) from A(5, 1) and B(-1, 5) are equal
- Find a relation between x and y if the points A(x, y), B(-4, 6) and C(-2, 3) are collinear
- If the points A(2, 3), B(-5, 6), C(6, 7) and D(p, 4) are the vertices
- Find the coordinates of the point which divides the join of A(-1, 7) and B(4, -3) in the ratio 2 : 3