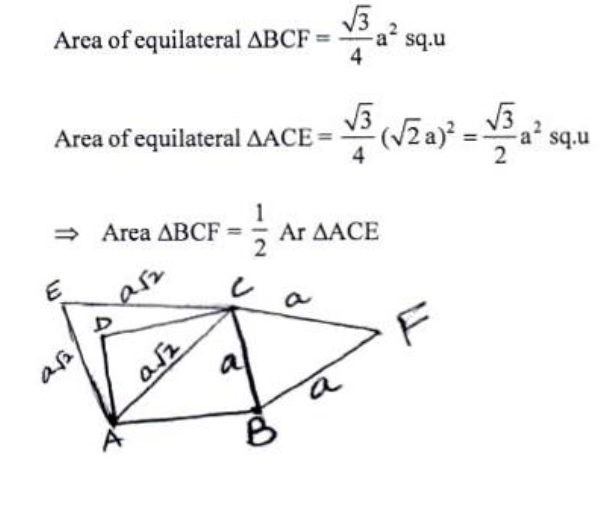
Prove that the area of an equilateral triangle described on one side of the square is equal
Triangles (10)Prove that the area of an equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonal.
Answer
Let the side of the square be a units
AC2 = a2 + a2 = 2a2
AC = $ \sqrt{2} a $ units
- Exam Year: 2018
Related Questions
- Two right triangles ABC and DBC are drawn on the same hypotenuse BC
- Observe the figures given below carefully and answer the questions
- Diagonals of a trapezium PQRS intersect each other at the point O
- In the adjoining figure, A, B and C are points on OP, OQ and OR
- DE II BC. Find the length of side AD, given that AE = 1.8 cm
- In an equilateral $\triangle$ ABC, D is a point on side BC such that BD