In the adjoining figure, A, B and C are points on OP, OQ and OR

Triangles (10)

In the adjoining figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC| | QR.

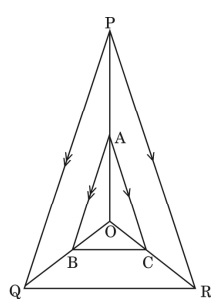
Answer

$$ \text{In } \triangle POQ, AB \parallel PQ $$

By Thales Theorem,

$$ \Rightarrow \frac{OA}{AP} = \frac{OB}{BQ} $$

$$ \text{In } \triangle POR, AC \parallel PR $$

$$ \Rightarrow \frac{OA}{AP} = \frac{OC}{CR} $$

From (i) and (ii),

$$ \frac{OB}{BQ} = \frac{OC}{CR} $$

$$ \therefore \triangle QOR, BC \parallel QR $$

(By converse of Thales theorem)

Exam Year: 2023
Related Questions