Write all the values of p for which the quadratic equation $x^2 + px + 16 = 0$
Quadratic Equations (10)Write all the values of p for which the quadratic equation x2 + px + 16 = 0 has equal roots. Find the roots of the equation so obtained.
Answer
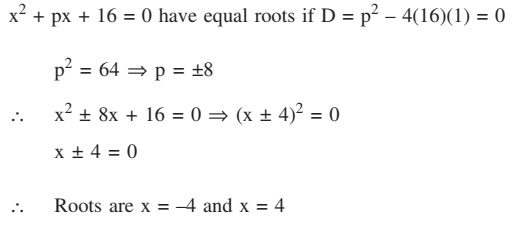
- Exam Year: 2019
Related Questions
- Find the nature of roots of the quadratic equation $2x^2 – 4x + 3 = 0$
- If the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k - 1, 5k) are collinear, then find the value of k
- Which of the following is not a quadratic equation
- Solve for x: $\frac{1}{x+1} +\frac{3}{5x+1} = \frac{5}{x+4}, x\ne-1, -\frac{1}{5}, -4$
- Find the roots of the quadratic equation $x^2 − x − 2 = 0 $
- A quadratic equation whose one root is 2 and the sum of whose roots is zero, is