In the adjoining figure, PT is a tangent at T to the circle with centre O. If $ \angle TPO = 30^o $, find the value of x
Circles (10)In the adjoining figure, PT is a tangent at T to the circle with centre O. If $ \angle TPO= 30^o $, find the value of x.
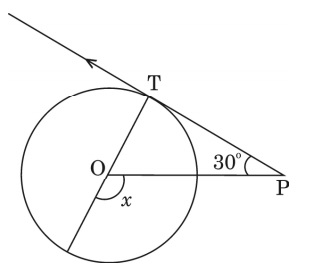
Answer
Tangent ⊥ radius at the point of contact
$$ \angle OTP = 90^0 $$
$$ x = 120^0 $$
- Exam Year: 2023
Related Questions
- If the angle between two tangents drawn from an external point P to a circle of radius a and centre O
- The length of the tangent from an external point A to a circle
- A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA
- Two concentric circles with centre O are of radii 3 cm and 5 cm
- In the given figure, XY and X'Y'are two parallel tangents to a circle with centre O
- Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord