In the given figure, XY and X'Y'are two parallel tangents to a circle with centre O

Circles (10)

In the given figure, XY and X'Y'are two parallel tangents to a circle with centre O and another tangent AB with point of contact C, is intersecting XY at A and X'Y' at B. Prove that $\angle AOB = 90^{\circ}$

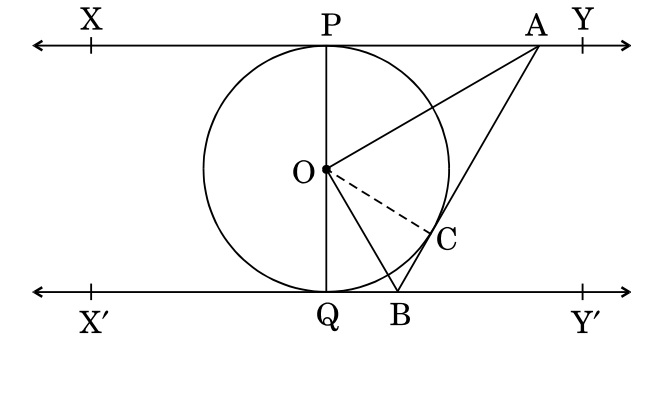
Answer

$$ \text{In right angled } \Delta POA \text{ and } \Delta OCA $$

$$ \Delta OPA \cong \Delta  \Delta OCA $$

$$ \angle POA = \angle AOC ...(i) $$

$$ \text{Also } \Delta OQB \cong \Delta \Delta OCB $$

$$ \angle QOB = \angle BOC....(ii) $$

$$ \angle AOB = \angle AOC + \angle COB $$

$$ = \frac{1}{2} \angle POC +\frac{1}{2} \angle COQ $$

$$ = \frac{1}{2}(\angle POC + \angle COQ) $$

$$ = \frac{1}{2} \times 180^{\circ} $$

$$ = 90^{\circ} $$

• Exam Year: 2017