Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord

Circles (10)

Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.

Answer

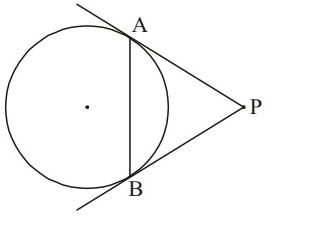
Case I:

Since PA = PB

Therefore in ΔPAB

∠PAB= ∠PBA 

Case II:

If the tangents at A and B are parallel then each angle between chord and tangent = 90°

  • Exam Year: 2017
Related Questions