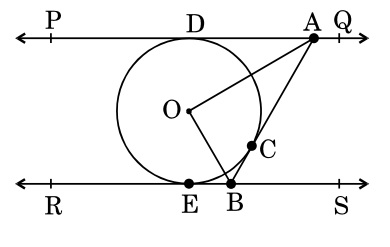
PQ and RS are two parallel tangents to a circle with centre O
Circles (10)PQ and RS are two parallel tangents to a circle with centre O and another tangent AB with point of contact C intersecting PQ at A and RS at B. Prove that ∠AOB = 90°.
Answer
Exam Year:
2019
Related Questions
- Two concentric circles with centre O are of radii 3 cm and 5 cm
- In the adjoining figure, PT is a tangent at T to the circle with centre O. If $ \angle TPO = 30^o $, find the value of x
- A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA
- The length of the arc of a circle of radius 14 cm which subtends an angle of
- Prove that the lengths of tangents drawn from an external point to a circle are equal
- How many tangents can be drawn to a circle from a point on it