A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA
Circles (10)A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA.
Answer
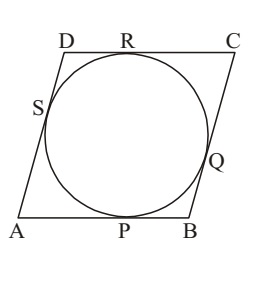
Here AP = AS
BP = BQ
CR = CQ
DR = DS
Adding,
(AP + PB) + (CR + RD) = (AS + SD) + (BQ + QC)
AB + CD = AD + BC
- Exam Year: 2017
Related Questions
- Prove that the lengths of tangents drawn from an external point to a circle are equal
- If the angle between two tangents drawn from an external point P to a circle of radius a and centre O
- How many tangents can be drawn to a circle from a point on it
- PQ and RS are two parallel tangents to a circle with centre O
- Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord
- Two concentric circles with centre O are of radii 3 cm and 5 cm