$\sin^2 60^{\circ} + 2 \tan 45^{\circ} – \cos^2 30^{\circ} $
Trigonometry (10)Evaluate: $\sin^2 60^{\circ} + 2 \tan 45^{\circ} – \cos^2 30^{\circ} $
Answer
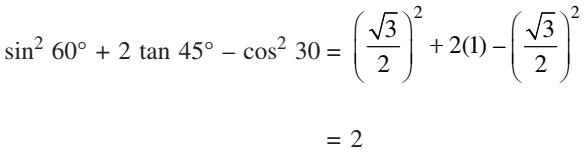
- Exam Year: 2019
Related Questions
- On a straight line passing through the foot of a tower, two points C and D
- The value of $ 5 \sin^2 90^{\circ} - 2 cos^20^{\circ} $ is
- As observed from the top of a 100 m high light house
- Prove that: $ \frac{\sin A - 2 \sin^3 A} {2 \cos^3 A – \cos A} = \tan A $
- What is the value of $(cos^2 67° - sin^2 23°)$
- If $ \sin\alpha = \frac{1}{2} $, then find the value of $ 3 \cos \alpha − 4 cos^3 \alpha $