On a straight line passing through the foot of a tower, two points C and D
Trigonometry (10)On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower.
Answer
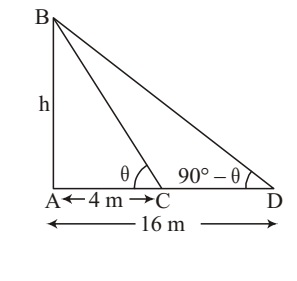
$$ \text{tan} $\theta = \frac{h}{4} $$
$$ \text{tan} (90 - \theta) = \frac{h}{16} $$
$$ \text{cot} \theta = \frac{h}{16} $$
Solving (i) and (ii) to get
h2 = 64
h = 8 m
- Exam Year: 2017
Related Questions
- As observed from the top of a 100 m high light house
- If $ \sin\alpha = \frac{1}{2} $, then find the value of $ 3 \cos \alpha − 4 cos^3 \alpha $
- The angle of elevation of the top of a 30 m high tower
- Prove that: $\frac{\tan\theta} {1- \cot\theta}$ + $\frac{\cot\theta}{1-\tan\theta}$ = $1 + \sec\theta \csc\theta$
- If a tower 30 m high, casts a shadow $10\sqrt{3}$ m long on the ground
- $ If 4 \tan \theta = 3, evaluate \frac{4 \sin\theta - \cos\theta + 1}{4 \sin\theta + \cos \theta - 1}$